Command manual

Introduction and some definitions

This is a concrete model with different failure mechanisms in compression and tension. There is one damage variable for tensile damage $D_t$ and one for crushing damage $D_c$. $D_t$ is driven by inelastic deviatoric deformations and $D_c$ by dilatation and deviatoric deformations. The variables run from $0$ (undamaged material) to $1$ (fully damaged material).

Inelastic deformation is a combination of shearing and dilatation. Deviatoric inelastic strains eventually lead to the formation of macroscopic cracks $(D_t = 1)$. Node splitting can be used for the representation of such cracks.

The deviatoric flow stress is a function of both pressure $p$ and Lode angle $\theta$. At a given pressure level (for an undamaged material), the ratio between the flow stresses at $\theta=60^\circ$ and $\theta=0$ is defined as:

$\displaystyle{ \frac{\sigma_y(p,\theta=60^\circ)}{\sigma_y(p, \theta=0)} = 1 + \left( \frac{1}{e} - 1 \right) \cdot \left( 1 - 2z + z^2 \right) }$

where:

$\displaystyle{ z(p) = \frac{p - p_s}{\xi p_0 - p_s} }$

$\frac{1}{2} \leq e \leq 1$ is an input parameter controlling the magnitude of the Lode angle dependency and $p_s$ is a yet undetermined minimum (negative) pressure value at which the deviatoric flow stress $\sigma_y=0$. This equation is only valid in the range $0 \leq z \leq 1$. The ratio is $1/e$ at $p=p_s$ and gradually drops to $1$ at $p=\xi p_0$. The flow stress also increases with increasing pressure. The relationship is assumed be linear (for Lode angle $\theta=0^\circ$) between $p=p_s$ and $p=f_c/3$:

$\displaystyle{ \frac{\partial \sigma_y(p, \theta=0)}{\partial p} = \eta }$

Here $\eta$ is also an unknown parameter that needs to be derived. A schematic picture of the relationship between failure stress, pressure $p$ and Lode angle $\theta$ is shown in the figure below. Note that uni-axial tensile loading corresponds to $\theta=0^\circ$ and uni-axial compression to $\theta=60^\circ$.

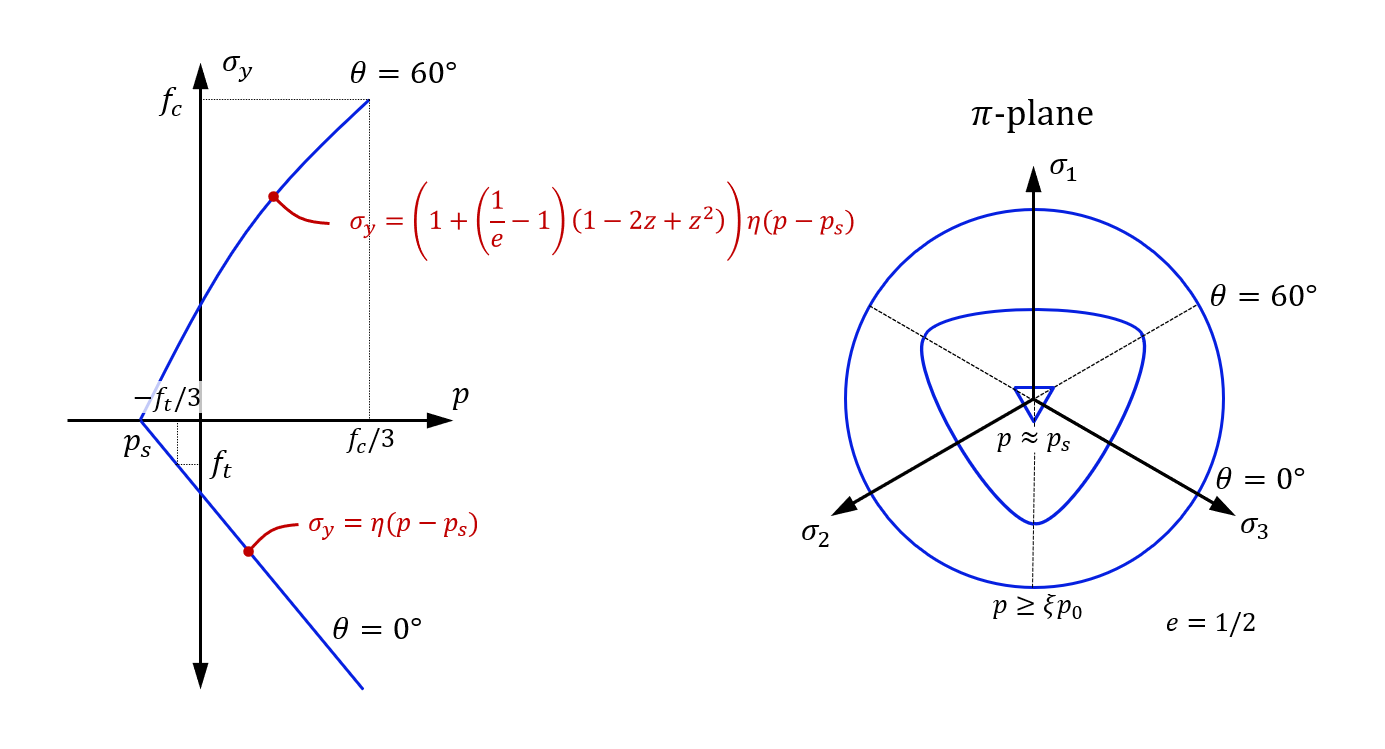
We know that the quasi-static uni-axial tensile failure stress is $f_t$ and that the uni-axial compressive failure stress is $f_c$. Hence, the equation system to solve, in order to find $p_s$ and $\eta$ is:

$\displaystyle{ f_t = \eta \left(-\frac{f_t}{3} - p_{s0} \right) }$

$\displaystyle{ f_c = \left( 1 + \left( \frac{1}{e} - 1 \right) \cdot \left( 1 - 2 z\left( f_c/3 \right) + z \left( f_c/3 \right)^2 \right) \right) \cdot \eta \left( \frac{f_c}{3} - p_{s0} \right) }$

That is, the user inputs $f_t$, $f_c$, $e$, $p_0$, $\xi$ and the solver will find $\eta$ and $p_{s0}$. $p_{s0}$ is the quasi-static value of $p_s$ for an undamaged material. The connection between $p_s$, $p_{s0}$, strain rate and damage is defined below.

Elastic and viscous stresses

The total stress $\boldsymbol\sigma$ is the sum of an elastic component $\boldsymbol\sigma^e$ and a viscous component $\boldsymbol\sigma^v$.

$\boldsymbol\sigma = \boldsymbol\sigma^e + \boldsymbol\sigma^v$

where:

$\boldsymbol\sigma^e = 2G \boldsymbol\varepsilon_{dev}^e + K \varepsilon_{vol}^e \mathbf{I}$

$\boldsymbol\varepsilon_{dev}^e$ is the deviatoric elastic strain, $K$ is the bulk modulus (defined below) and $\varepsilon_{vol}^e$ is the elastic volumetric strain. The viscous stress component is defined as:

$\displaystyle{ \boldsymbol\sigma^v = c_{dev} \left( \left( 1 + \frac{\vert \dot{\boldsymbol\varepsilon}_{dev} \vert}{\dot{\varepsilon}_{0}} \right)^v - 1 \right) \frac{\dot{\boldsymbol\varepsilon}_{dev}}{\vert \dot{\boldsymbol\varepsilon}_{dev} \vert} + c_{vol} \left( \left( 1 + \frac{\vert \dot{\varepsilon}_{vol} \vert}{\dot{\varepsilon}_{0}} \right)^v - 1 \right) \frac{\dot{\varepsilon}_{vol}}{\vert \dot{\varepsilon}_{vol} \vert} {\bf I}}$

where $\dot{\boldsymbol \varepsilon}_{dev}$ is the total deviatoric strain rate and $\dot{\varepsilon}_{vol}$ is the volumetric strain rate. $\dot{\varepsilon}_{0}$ is a reference strain rate (hardcoded to $1 s^{-1}$).

Compaction

The flow criteria (in both tension and compression) are evaluated using the elastic stresses. In pure hydrostatic loading the elastic bulk modulus $K$ and the compaction pressure $p_c$ are assumed to grow with the inelastic compaction strain $\varepsilon_{vol}^p$:

$\displaystyle{ K = \left( 1 - \frac{\varepsilon_{vol}^p}{\varepsilon_L} \right) K_0 + \frac{\varepsilon_v^p}{\varepsilon_L} K_L}$

$\displaystyle{ p_c = p_0 + ( p_L - p_0 ) \left( \frac{\varepsilon_{vol}^p}{\varepsilon_L} \right)^n + r_f (\dot\varepsilon_v^p)^{r_e}}$

The volumetric compaction strain $\varepsilon_{vol}^p$ can not exceed $\varepsilon_L$.

Compaction normally occurs in mixed stress states involving both crushing and deviatoric shear flow. This process takes place on the so called yield surface cap (explained later).

Deviatoric flow stress

The deviatoric flow stress $\sigma_y$ is a function of pressure $p$, Lode angle $\theta$, damage parameters $D_t, D_c$ (softening) and of the effective plastic strain $\varepsilon_{eff}^p$ (hardening):

$\displaystyle{\sigma_y = \mathrm{min} \left( S_{max} \cdot f_c, f(p) \cdot g({\varepsilon_{eff}^p}) \cdot h(p, \theta, D_t, D_c) \right)}$

$f(p)$ is the ultimate deviatoric flow stress versus pressure at Lode angle $\theta=0$, $g(\varepsilon_{eff}^p)$ describes the strain hardening and $h(p, \theta, D_t, D_c)$ is a Lode angle scale factor. $S_{max}$ is an optional diemsionless parameter that offers the possibility to define an upper limit for the deviatoric flow stress.

The pressure dependence function $f(p)$ is defined as:

$\displaystyle{f(p) = \left\{ \begin{array}{ccc} \eta \left( p - p_s \right) & : & p \leq \frac{f_c}{3} \\ \eta \left( p - p_s - \frac{1}{2} \frac{(p - \frac{f_c}{3})^2}{\xi p_c - \frac{f_c}{3}} \right) & : & \frac{f_c}{3} \lt p \leq \xi p_c \\ \eta \left( \frac{\xi p_c}{2} - p_s + \frac{f_c}{6} \right) & : & p > \xi p_c \end{array} \right. }$

where:

$\displaystyle{ \eta = \frac{3}{2} \cdot \frac{f_c - 2f_t}{f_t + f_c} }$

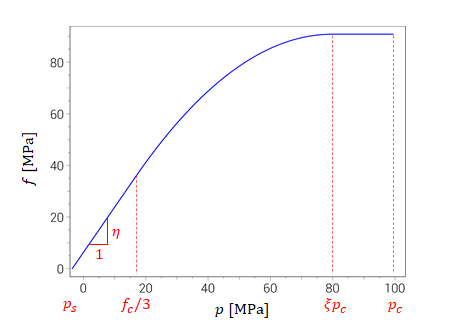
The material hardening factor $g(\varepsilon_{eff}^p)$ starts at $\xi_y$ (yield surface) and ramps up linearly with plastic strain to $1$ (failure surface):

$\displaystyle{\dot{g}(\dot{\varepsilon}_{eff}^p) = \left\{ \begin{array}{ccc} \left( 1 - \xi_y \right) \cdot \frac{\dot{\varepsilon}_{eff}^p}{\varepsilon_u} & : & g \lt 1 \\ 0 & : & g = 1 \end{array} \right. }$

$\displaystyle{g(0) = \xi_y }$

The effective plastic strain at peak stress $\varepsilon_u$ is pressure dependent:

$\displaystyle{ \varepsilon_u = \left\{ \begin{array}{ccc} (1 - \xi_u) \varepsilon_{ut} + \xi_u \varepsilon_{uc} & : & \xi_u \leq 1 \\ \varepsilon_{uc} + \left( (\xi_u-1) - \frac{1}{2} (\xi_u-1)^2 \right) \cdot \left( \varepsilon_{uc} - \varepsilon_{ut} \right) & : & 1 \leq \xi_u \leq 2 \\ \varepsilon_{uc} + \frac{1}{2} \left( \varepsilon_{uc} - \varepsilon_{ut} \right) & : & \xi_u > 2 \end{array} \right. }$

where:

$\displaystyle{ \xi_u = \frac{3p + f_t}{f_c + f_t} }$

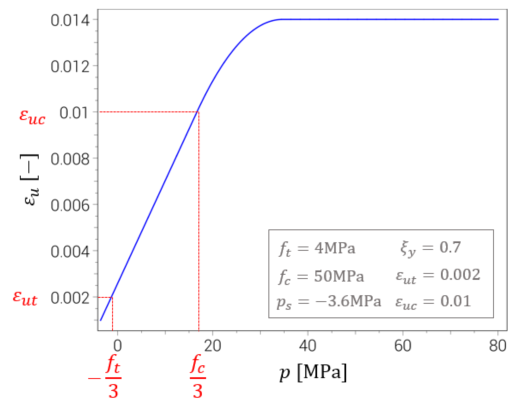
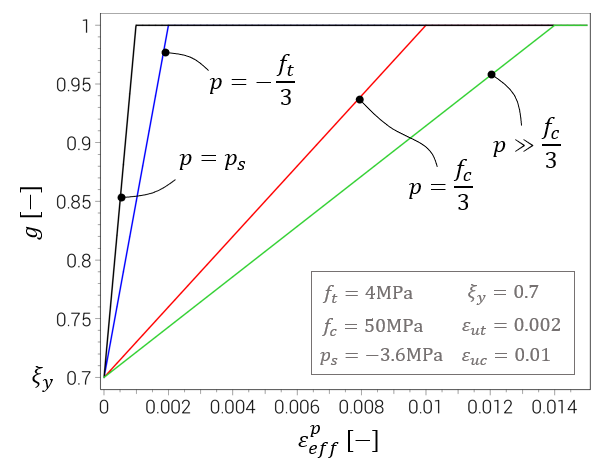
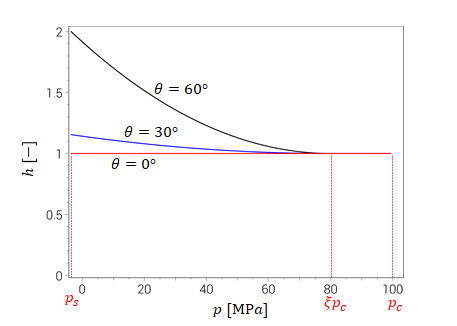
The Lode angle dependency $h(p, \theta, D_t, D_c)$ is stronger at low (or negative pressures) and is weakend by increaing pressure and material damage.

$\displaystyle{ h(p, \theta, D_t, D_c) = \left\{ \begin{array}{ccc} \left[ 1 + \frac{1-e}{e} \cdot \left( \frac{1}{\mathrm{cos}(\theta)} - 1 \right) \cdot \left( 1 - 2z + z^2 \right) \cdot (1 - D_c^2) \right] \cdot \left[ 1 + (\xi_y-1) \cdot D_t \right] & : & z \leq 1 \\ 1 + (\xi_y-1) \cdot D_t & : & z > 1 \end{array} \right. }$

where:

$\displaystyle{ z = \frac{p - p_s}{\xi p_c - p_s} }$

$\displaystyle{ p_s = \left( p_{s0} - \frac{r (\dot\varepsilon_{eff}^p)^s}{\eta} \right) \cdot (1 - D_t) \cdot (1 - D_c)}$

$\theta$ is the Lode angle, as defined in the figure below. Note that $p_s=0$ for a fully damaged material.

Yield surface

The yield criterion is separated into two regions in stress space. At pressures below $\xi p_c$ the flow is mainly deviatoric. Any inelastic volumetric strains are going to be positive (bulking). The second region is referred to as the cap. Plastic flow on the cap can be a combination of both volumetric crushing and deviatoric shear flow.

Typical projections of the yield surface (at $\theta=0$ and $\theta=60^\circ$) are shown in the picture below.

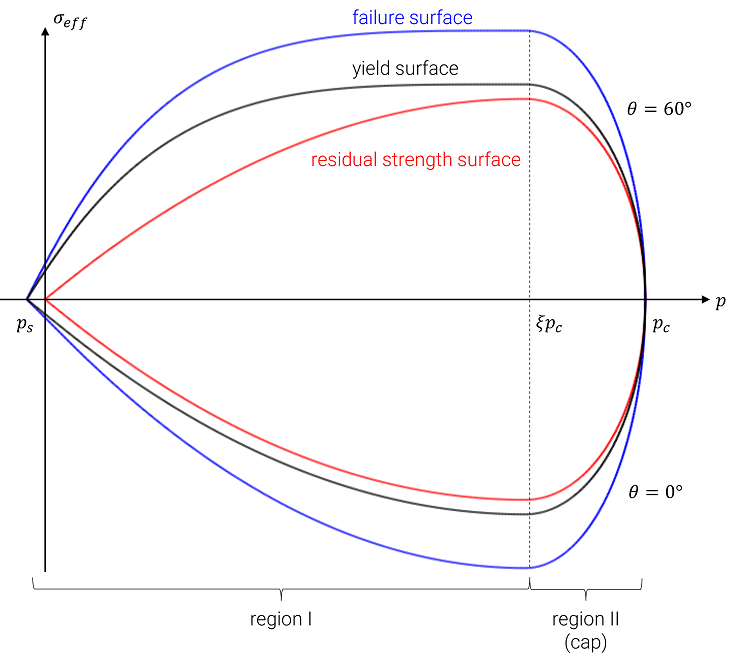
Region I

The plastic flow criterion in region I (see figure below) is purely deviatoric. Yielding occurs when the (J2) effective stress reaches $\sigma_y$ (as defined above).

$\displaystyle{ \sigma_{eff} = {\sigma_y} \Rightarrow \mathrm{Yielding} }$

Default plastic flow direction is purely deviatoric. However, bulking can be activated by setting bulk=1.

Region II (cap)

In region II (cap region) plastic flow incorporates both crushing and inelastic deviatoric strains (associated flow rule). The flow criterion is satisfied when:

$\displaystyle{ \left(\frac{\sigma_{eff}}{\sigma_y}\right)^2 + \left(\frac{p / p_c -\xi}{1-\xi}\right)^2 = 1 \Rightarrow \mathrm{Yielding} }$

Damage evolution

Damage grows with inelastic deformation, but the process does not begin until reaching the failure surface $(g=1)$. From this point volumetric crushing damage $D_c$ growth is defined as:

$\displaystyle{\dot{D}_c = \frac{\dot\varepsilon_{eff}^p + \dot\varepsilon_{vol}^p}{\varepsilon_{fc} - \varepsilon_{u}}}$

and the evolution of tensile damage as:

$\displaystyle{\dot{D}_t = \frac{\dot\varepsilon_{eff}^p}{\varepsilon_{ft}}}$

$\displaystyle{ \varepsilon_{ft} = \frac{(1 - \xi_u) G_t + \xi_u G_c}{(1 - \xi_u) f_t + \xi_u f_c} \cdot \frac{2}{V_{ip}^{1/3}} }$

where $V_{ip}$ is the material volume represented by the local element integration point.