Command manual

This is a visco-elastic model for fabric materials. The model is easy to use in that no fiber directions need to be defined.

The total stress $\boldsymbol{\sigma}$ is the sum of a rate independent elastic stress tensor $\boldsymbol{\sigma}_e$ and a viscous deviatoric stress tensor $\boldsymbol{\sigma}_v$.

$\boldsymbol{\sigma} = \boldsymbol{\sigma}_e + \boldsymbol{\sigma}_v$

The elastic principal stresses are defined as:

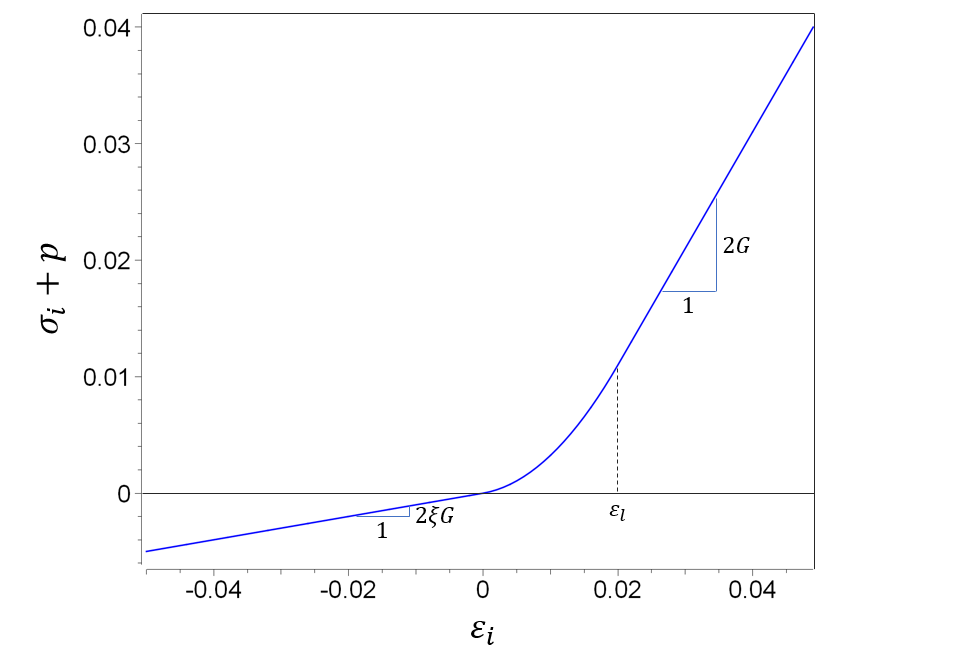
$\sigma_i = \left\{ \begin{array}{lcl} \displaystyle{ 2G \cdot \xi \cdot \varepsilon_i^{dev} - p} & : & \varepsilon_i^{dev} \leq 0 \\ \displaystyle{ 2G \cdot \left( \frac{1-\xi}{2} \cdot \frac{(\varepsilon_i^{dev})^2}{\varepsilon_l} + \xi \cdot \varepsilon_i^{dev} \right) - p} & : & 0 \lt \varepsilon_i^{dev} \leq \varepsilon_l \\ \displaystyle{ 2G \cdot \left( \frac{\xi-1}{2} \cdot \varepsilon_l + \varepsilon_i^{dev} \right) - p} & : & \varepsilon_i^{dev} \gt \varepsilon_l \end{array} \right. $

Here $\sigma_i, \; i=[1,3]$ is a principal stress and $\varepsilon_i^{dev}$ is a principal deviatoric strain. The corresponding principal directions are $\mathbf{n}_i$ and the rate independent stress tensor $\boldsymbol{\sigma}_e$ can be expressed as:

$\boldsymbol{\sigma}_e = \displaystyle{ \sum_{i=1}^3 \sigma_i \mathbf{n}_i \otimes \mathbf{n}_i }$

The pressure $p$ is a linear function of the volumetric strain $\varepsilon_v$:

$p = -K \varepsilon_v$

The viscous stresses $\boldsymbol{\sigma}_v$ are purely deviatoric and are controlled by parameters $c$ and $c_{dec}$.

$\boldsymbol{\sigma}_v(t) = \displaystyle{ \frac{2 c}{c_{dec}} \int_0^t \dot{\boldsymbol{\varepsilon}}_{dev}(\tau) \mathrm{e}^{(\tau-t)/c_{dec}} \mathrm{d}\tau }$

Here $t$ is the current time and $\dot{\boldsymbol{\varepsilon}}_{dev}$ is the deviatoric strain rate. Note that, given a constant deviatoric strain rate $\dot{\boldsymbol{\varepsilon}}_{dev}$, the viscous stress response will asymptotically approach:

$\displaystyle{ \lim_{t \to \infty} \boldsymbol{\sigma}_v = {2 c} \dot{\boldsymbol{\varepsilon}}_{dev} }$