MAT_GRANULAR_CAP
FE
SPH
Material properties
"Optional title"
mid, $\rho$, $E$, $\nu$
cid${}_1$, cid${}_2$, $\xi$, $\eta$, $\sigma_{dev}^{max}$, $B_0$, $B_1$
Parameter definition
Description
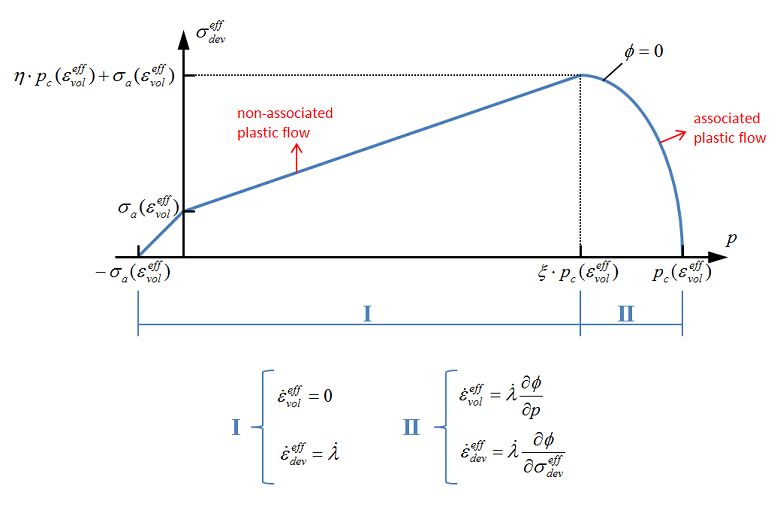
This is a material model for granular media, where inelastic deviatoric flow and volumetric flow are coupled. The shape of the yield surface is shown in the figure below. Note that the yield surface is split into two regions (I) and (II). Volumetric flow (compaction) is assumed to only occur in region II (associated flow). Plastic flow in region I is purely deviatoric (J2). In region II the surface is elliptic:
$\Phi = \displaystyle{\sqrt{ \left( \frac{\sigma_{dev}^{eff}}{\xi p_c + \sigma_a}\right)^2 + \left( \frac{p - \xi p_c}{p_c-\xi p_c}\right)^2 }} - 1$
cid${}_1$ describes the compaction pressure as function of the inelastic volumetric strain:
$p_c = \hat p_c(\varepsilon_{vol}^{eff})$.
cid${}_2$ describes the grain adhesion due to compaction (see yield surface in figure):
$\sigma_a = \hat\sigma_a(\varepsilon_{vol}^{eff})$.
Damage $D$ is assumed to grow at inelastic deviatoric deformations in region I:
$\displaystyle{ \dot D = \frac{ \dot\varepsilon_{dev}^{eff}}{B_0} \left( 1 - \frac{p}{p_c} \right)^{B_1}}$
Damage falls back to zero whenever the material undergoes further compaction (region II). As $D$ reaches 1 the adhesive components of the yield stress are set to zero and pressure is not allowed to drop below 0.
$D$ is set to 1 (instant failure) if meeting the pressure cut-off criterion, i.e. if $p = -\sigma_a$.