Command manual

This command is used to define pressure loads from underwater explosions. The command is based on semi-empirical equations as suggested by Geers and Hunter (An integrated wave-effects model for an underwater explosion bubble, Journal of the Acoustical Society of America, 2002).

Pressure loads from both the initial shock wave and from the following bubble osciallations are generated.

Shock phase

During the shock phase the incident pressure at a distance $L$ from the bubble center is defined as:

$\displaystyle{p(L,t) = \frac{\rho_w}{4 \pi L} \left( \frac{R_c}{L} \right)^A \ddot{V}( \left[ R_c/L \right]^B t)}$

where $\rho_w$ is the water density, $R_c$ is the initial charge radius, $R$ is the current bubble radius and $V$ is the bubble volume:

$\displaystyle{ R_c = \left( \frac{3 m_{HE}}{4 \pi \rho_{HE}} \right)^{1/3} }$

$\displaystyle{V(t) = \frac{4}{3} \pi R_c^3 + \frac{4 \pi R_c}{\rho_w} \left[ 1.5857 \frac{t}{t_c} - 5.8293 + 0.4609 \mathrm{e}^{-1.338 t/t_c} + 5.3684 \mathrm{e}^{-0.1805 t/t_c} \right] p_c t_c^2}$

$\displaystyle{ t_c = \frac{R_c}{v_c} }$

Oscillation phase

The oscillation phase is assumed to begin at time $t_i = 7 t_c$. During the oscillation phase the bubble radius $R$ and its vertical migration $u$ are assumed to evolve according to:

$\displaystyle{\dot{R} = -\frac{\phi_{l0}}{R} -\frac{1}{c_w} \left( \dot{\phi}_{l0} - \dot{R}^2 - \frac{1}{3}\dot{u}^2 - \frac{2}{3}\dot{u}\frac{\phi_{l1}}{R} \right) }$

$\displaystyle{\dot{u} = -2 \frac{\phi_{l1}}{R} -\frac{1}{c_w} \left( \dot{\phi}_{l1} - 2 \dot{R} \dot{u} \right) }$

where:

$\displaystyle{\dot{\phi}_{l0} = \frac{1}{1 + \zeta} \left[ \left( \frac{1}{2} + \frac{\rho_g}{2\rho_w} + \zeta \right) \left( \dot{R}^2 + \frac{\dot{u}^2}{3} \right) - \frac{\rho_g}{\rho_w} c_g \frac{\phi_{l0}}{R} + \frac{2}{3} \left( 1 + \zeta \right) \dot{u} \frac{\phi_{l1}}{R} - Z \right] }$

$\displaystyle{\dot{\phi}_{l1} = \frac{1}{1 + \zeta} \left[ \left( 1 + \frac{\rho_g}{\rho_w} + 2 \zeta \right) \dot{R} \dot{u} -\left( 1 - \frac{\rho_g}{\rho_w} \right) g R - \frac{\rho_g}{\rho_w} c_g \frac{2 \phi_{l1} + \phi_{g1}}{R} + \frac{3}{8} C_d \vert \dot{u} \vert^{E_d} \dot{u}_0^{2-E_d} \right] }$

$\displaystyle{\dot{\phi}_{g1} = \frac{1}{1 + \zeta} \left[ \left( 2 + \frac{c_g}{c_w} + \zeta \right) \dot{R} \dot{u} - \frac{c_g}{c_w} \left( 1 - \frac{\rho_g}{\rho_w} \right) g R - c_g \frac{2 \phi_{l1} + \phi_{g1}}{R} - \frac{3 c_g}{8 c_w} C_d \vert \dot{u} \vert^{E_d} \dot{u}_0^{2-E_d} \right] }$

$\displaystyle{ Z = \frac{1}{\rho_w} \left( p_g - p_i + \rho_w g u \right) + \frac{1}{3} \left[ \left( \frac{\phi_{l1}}{R} \right)^2 - \frac{\rho_g}{\rho_w} \left( \frac{\phi_{g1}}{R} \right)^2 \right] }$

$\displaystyle{ \zeta = \frac{\rho_g c_g}{\rho_w c_w} }$

$p_i$ is the initial hydrostatic pressure prior to detonation, $\rho_w$ is the water density, $\rho_g$ is the bubble gas density, $p_g$ is the bubble pressure, $c_w$ is the speed of sound in the water and $c_g$ is the current speed of sound in the gas.

$\displaystyle{ p_i = p_{atm} + \rho g d }$

$\displaystyle{ p_g = K_c \left( \frac{R_c}{R} \right)^{3\gamma} }$

$\displaystyle{ \rho_g = \rho_{HE} \left( \frac{R_c}{R} \right)^3 }$

$\displaystyle{ c_g = \sqrt{\frac{\gamma K_c}{\rho_{HE}}} \left( \frac{R_c}{R} \right)^{\frac{3}{2}(\gamma-1)} }$

$p_{atm}$ is the atmospheric pressure and $g$ is the gravity constant. Initial conditions are:

$\displaystyle{ \phi_{l0}(t=t_i) = -R \dot{R} \left[ 1 - \frac{1}{2} \left( 1 - \frac{\rho_g}{\rho_w} \right) \frac{\dot{R}}{c_w} + \zeta \right] + \frac{R}{c_w} Z }$

$\displaystyle{ \phi_{l1}(t=t_i) = 0 }$

$\displaystyle{ \phi_{g1}(t=t_i) = -\left( 1 - \frac{\rho_g}{\rho_w} \right) \frac{g R^2}{\zeta c_w} }$

In the oscillation phase the incident pressure at distance $L$ from the center of the bubble is defined as:

$\displaystyle{ p(L,t) = \rho_w \frac{R^2 \ddot{R} + 2 R \dot{R}^2}{L} }$

Reflected pressure

The reflected pressure against a surface is:

$\displaystyle{ p_R(L,t) = p(L,t) \cdot \left( 1 + \mathrm{cos}(\alpha) \right) }$

$\alpha$ is the angle between the surface normal and the vector from the surface to the center of the bubble.

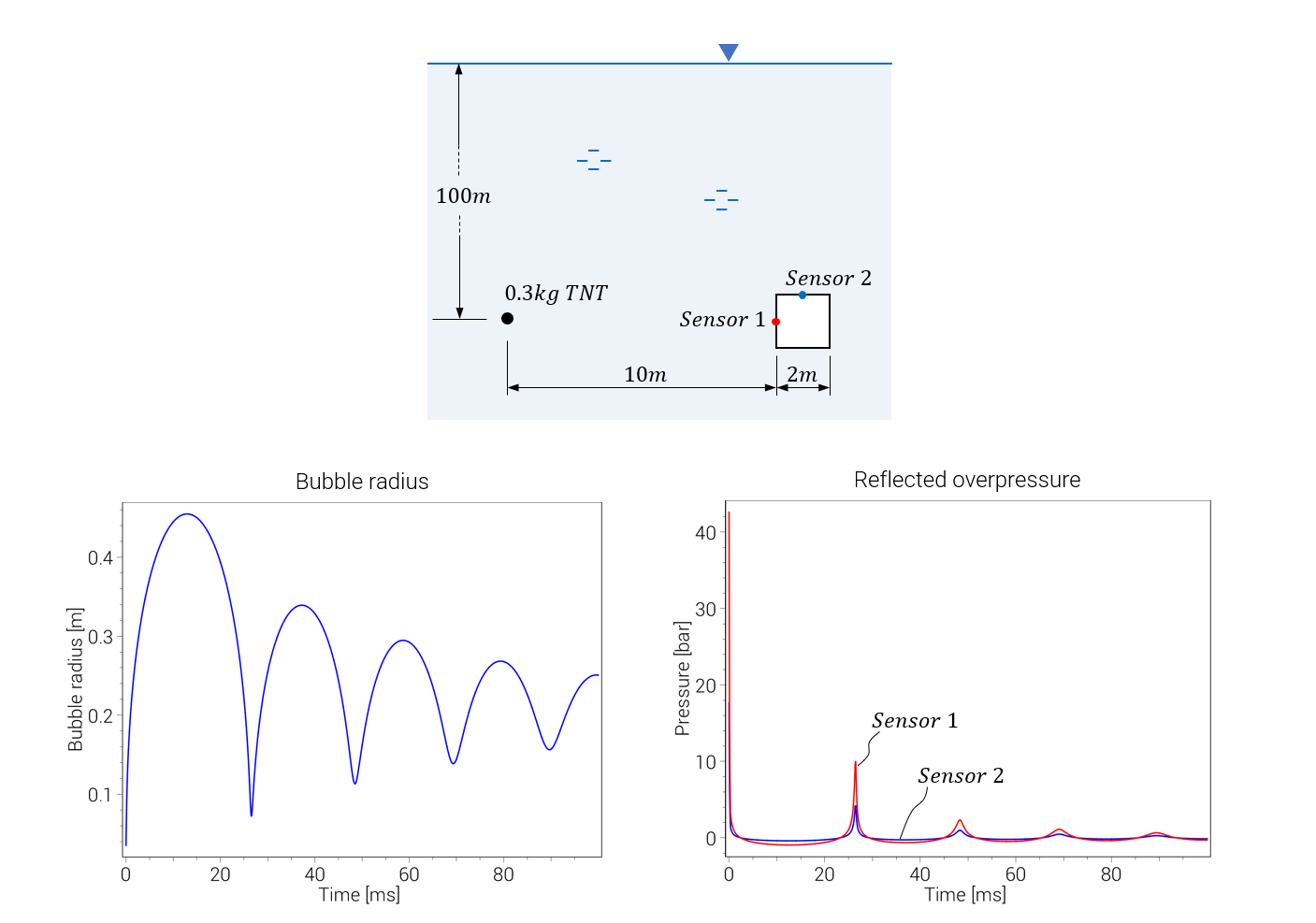
Underwater explosion (TNT)

A simple example of an underwater explosion using TNT parameters from Geers and Hunter (2002).