Command manual

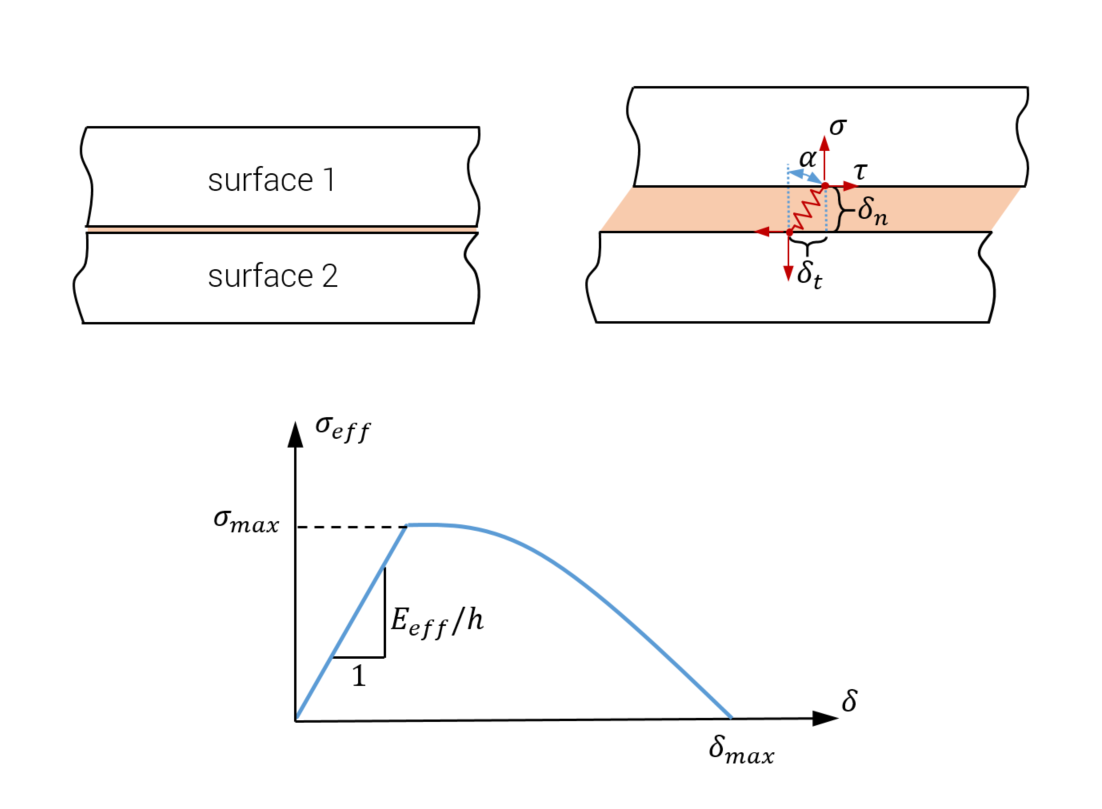
This command is used to define the effect of an adhesive between two surfaces. The glue is represented by a series of generalized spring elements connected between the nodes on Surface 1 and the element faces on Surface 2. The picture below shows stresses building up in one spring element. The shear stress $\tau$ is defined as:

$\displaystyle{ \tau = \frac{E}{2(1+\nu)} \cdot \frac{\delta_t}{h} }$

The normal stress component is:

$\displaystyle{ \sigma = \frac{(1-\nu)E}{(1+\nu)(1-2\nu)} \cdot \frac{\delta_n}{h} }$

A resultant (effective) stress measure in the spring is defined as:

$\displaystyle{ \sigma_{eff} = \sqrt{\sigma^2 + \tau^2} = \frac{E_{eff} \delta}{h} }$

where $E_{eff}$ is a direction dependent stiffness:

$\displaystyle{ E_{eff} = \sqrt{ \frac{(1-\nu)^2}{((1+\nu)(1-2\nu))^2} \cdot \mathrm{cos}^2 \alpha + \frac{1}{4(1+\nu)^2} \cdot \mathrm{sin}^2 \alpha } \cdot E }$

The definition of the loading angle $\alpha$ is shown in the figure below. $\sigma_f$ is the maximum stress in pure vertical loading and $\tau_f$ is the capacity in shear. The maximum effective stress $\sigma_{max}$ in a general direction of stretching is defined as:

$\displaystyle{ \sigma_{max}(\alpha) = \left( \sigma_f \cdot \mathrm{cos}^2 \alpha + \tau_f \cdot \mathrm{sin}^2 \alpha \right)}$

That is, damage will grow and the stresses will drop once $\sigma_{eff}$ reaches $\sigma_{max}$. Also the work of fracture $G$ is direction dependent. The elongation at complete fracture $\delta_{max}$ is adjusted such that:

$\displaystyle{ G(\alpha) = \frac{1}{2} \sigma_{max} \delta_{max} = G_I \cdot \mathrm{cos}^2 \alpha + G_{II} \cdot \mathrm{sin}^2 \alpha}$

Spring element representing adhesive between two surfaces