Command manual

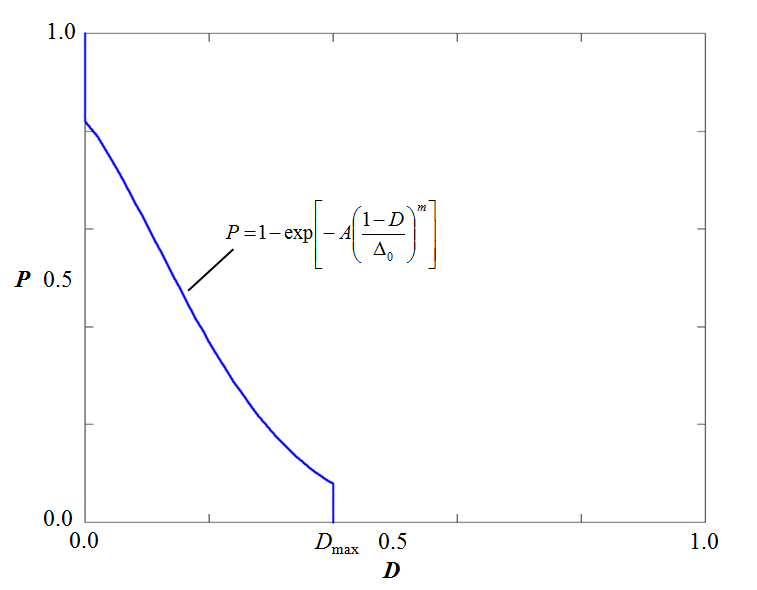
This command is used to define randomly distributed initial defects on the surface of a body. The defects are interpreted as equivalent to an initial damage $D$. The probability $P$ of having an initial defect larger or equal to $D$ on a surface $A$ is defined as:

$P(A,D) = \left\{ \begin{array}{lcl} 1 & : & D=0 \\ 1 - \mathrm{exp} \left[ -A \left( \displaystyle{\frac{1-D}{\Delta_0}} \right)^m \right] & : & 0 \lt D \le D_{max} \\ 0 & : & D \gt D_{max} \end{array} \right.$

The variables $\Delta_0, m$ and $D_{max}$ are input parameters that typically need to be tuned to match experimental data with a certain spread.

Typical initial damage probability function $P(A,D)$

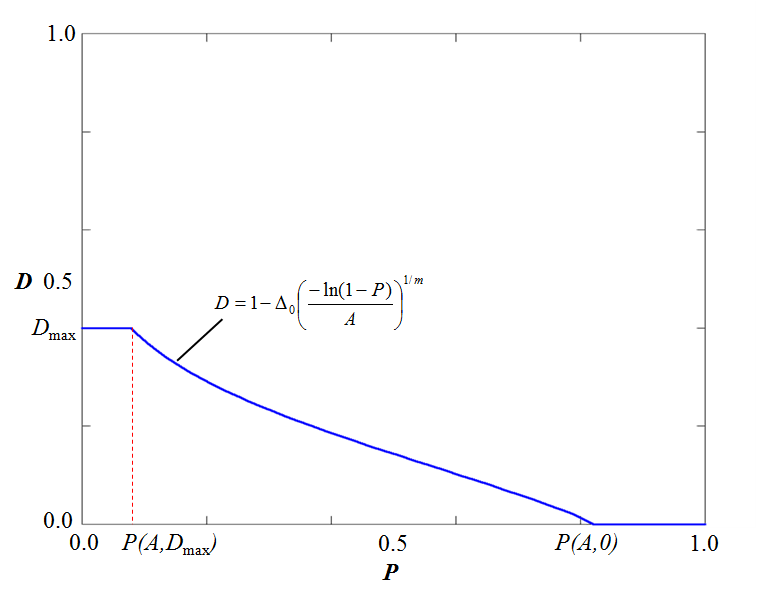
The inverse function $D(A,P)$ is used to define the intitial damage level for each integration point near the material surface. In this context $0 \le P \le 1$ is a random number and $A$ is the area represented by the integration point.

$D(A,P) = \left\{ \begin{array}{lcl} 0 & : & P \gt P(A,0) \\ 1 - \Delta_0 \left( \displaystyle{\frac{-\mathrm{ln}(1-P)}{A}} \right)^{1/m} & : & P(A,D_{max}) \lt P \le P(A,0) \\ D_{max} & : & P \lt P(A,D_{max}) \end{array} \right.$

Typical initial damage function $D(A,P)$