This is a material model for high strength steels and hard metals in ballistic applications. The total stress is the sum of an elastic stress $\boldsymbol{\sigma}^e$ and a viscous stress $\boldsymbol{\sigma}^v$.

$\displaystyle{ \boldsymbol{\sigma} = \boldsymbol{\sigma}^e + \boldsymbol{\sigma}^v }$

where

$\displaystyle{ \boldsymbol{\sigma}^e = -p {\bf{I}} + G \boldsymbol{\varepsilon}_{dev}^e }$

$\displaystyle{ \boldsymbol{\sigma}^v = \frac{1}{c_{dec}} \int_0^t g(\vert \dot{\boldsymbol{\varepsilon}}_{dev} \vert) \frac{\dot{\boldsymbol{\varepsilon}}_{dev}} {\vert \dot{\boldsymbol{\varepsilon}}_{dev} \vert} \mathrm{e}^{\frac{\tau-t}{c_{dec}}} \mathrm{d}\tau }$

$g$ is either a FUNCTION of viscous stress versus strain rate or, if defined through a constant $c$:

$g(\vert \dot{\boldsymbol{\varepsilon}}_{dev} \vert) = c \cdot \vert \dot{\boldsymbol{\varepsilon}}_{dev} \vert $

$p$ is the material pressure, $\boldsymbol{\varepsilon}_{dev}^e$ is the deviatoric part of the elastic strain tensor and $\dot{\boldsymbol{\varepsilon}}_{dev}$ is the total deviatoric strain rate. $G$ is the shear modulus.

$\displaystyle{ p = -K \varepsilon_v + 3 K \alpha (T-T_{ref})}$

$K$ is the bulk modulus, $\alpha$ is the thermal heat expansion coefficient and $T_{ref}$ is the reference temperature (defined in PROP_THERMAL). Note that the elastic properties can either be defined as constants or as functions of temperature. Yielding occurs when the effective elastic stress $\sigma_{eff}^e$ reaches the yield stress $\sigma_y$.

$\displaystyle{ \sigma_{eff}^e = \left[ \frac{1}{2}\left( \sigma_1^e - \sigma_2^e \right)^m + \frac{1}{2}\left( \sigma_2^e - \sigma_3^e \right)^m + \frac{1}{2}\left( \sigma_3^e - \sigma_1^e \right)^m \right]^{1/m} }$

$\displaystyle{ \sigma_y = \left[ \left( A(T) + B(T)\left(\varepsilon_{eff}^p\right)^{n(T)} \right) \cdot \left( 1 + s \right) + 3s \cdot p \right] \cdot \left[ 1 + \frac{\dot{\varepsilon}_{eff}^p}{\dot{\varepsilon}_r} \right]^{c_r} \cdot h(\bar\varepsilon_s) }$

In the yield stress expression $h(\bar\varepsilon_s)$ is a material softening function. Its purpose is to capture the effects of dynamic recrystallization or the formation of adiabatic shear bands.

$\displaystyle{ h(\bar\varepsilon_s) = \left\{ \begin{array}{ccc} 1 & : & \bar\varepsilon_s \leq \varepsilon_s \\ 1 - \eta_s\cdot(1-\mathrm{e}^{-c_s\cdot(\bar\varepsilon_s-\varepsilon_s)}) & : & \bar\varepsilon_s \gt \varepsilon_s \end{array} \right.}$

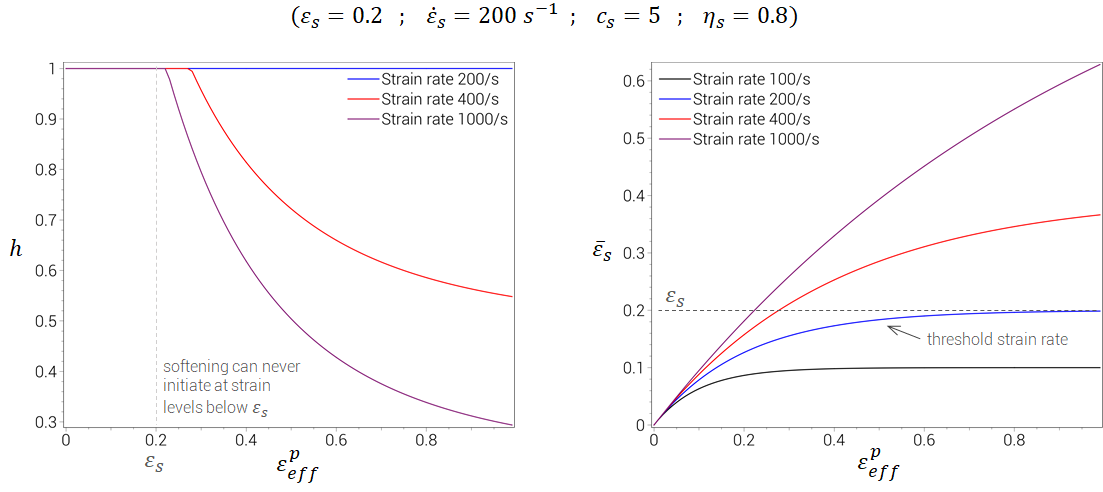
$\bar\varepsilon_s$ is a strain measure that grows faster at high effective plastic strain rates. It will never reach $\varepsilon_s$ (limit for onset of the softening process) if the plastic strain rate is below $\dot\varepsilon_s$. The curves below show how $\bar\varepsilon_s$ and the softening factor $h$ develop at different strain rates for a given set of input parameters.

$\displaystyle{ \bar\varepsilon_s = \int_0^t \dot{\varepsilon}_{eff}^p (\tau) \cdot \mathrm{e}^\frac{\dot{\varepsilon}_s \cdot (\tau-t)}{\varepsilon_s}\mathrm{d} \tau}$

Dynamic softening at different plastic strain rates.

A material that accounts for thermal softening

A simple example showing how certain parameters can be defined as functions of temperature. Note that this example does not represent a real alloy.