Command manual

This is a concrete model with different failure mechanisms in compression and tension. The material is assumed to have a pressure dependent shear resistance. Inelastic deformation is a combination of shearing and dilatation. Inelastic dilatation is interpreted as crushing that gradually reduces the shear resistance of the material. Deviatoric inelastic strains eventually lead to the formation of macroscopic cracks. Node splitting is used for the representation of such cracks. Note that node splitting can not occur in MERGE or REFINE interfaces.

The total stress $\sigma$ is the sum of an elastic component $\sigma^e$ and a viscous component $\sigma^v$.

$\sigma = \sigma^e + \sigma^v$

where:

$\sigma^e = 2G \varepsilon_{dev}^e - p \mathbf{I}$

$\varepsilon_{dev}^e$ is the deviatoric elastic strain and $p$ is the pressure. The viscous stress component is defined as:

$\sigma^v = c \dot\varepsilon$

where $\dot\varepsilon$ is the total strain rate. Note that the flow criteria (in both tension and compression) are evaluated using the elastic stresses. In hydrostatic loading the elastic bulk modulus $K$ and the compaction pressure $p_c$ are assumed to grow with the ineastic compaction strain $\varepsilon_v^p$:

$K = \left( 1 - \frac{\varepsilon_v^p}{\varepsilon_L} \right) K_0 + \frac{\varepsilon_v^p}{\varepsilon_L} K_L$

$\displaystyle{ p_c = p_0 + ( p_L - p_0 ) \left( \frac{\varepsilon_v^p}{\varepsilon_L} \right)^n + r_f (\dot\varepsilon_v^p)^{r_e}}$

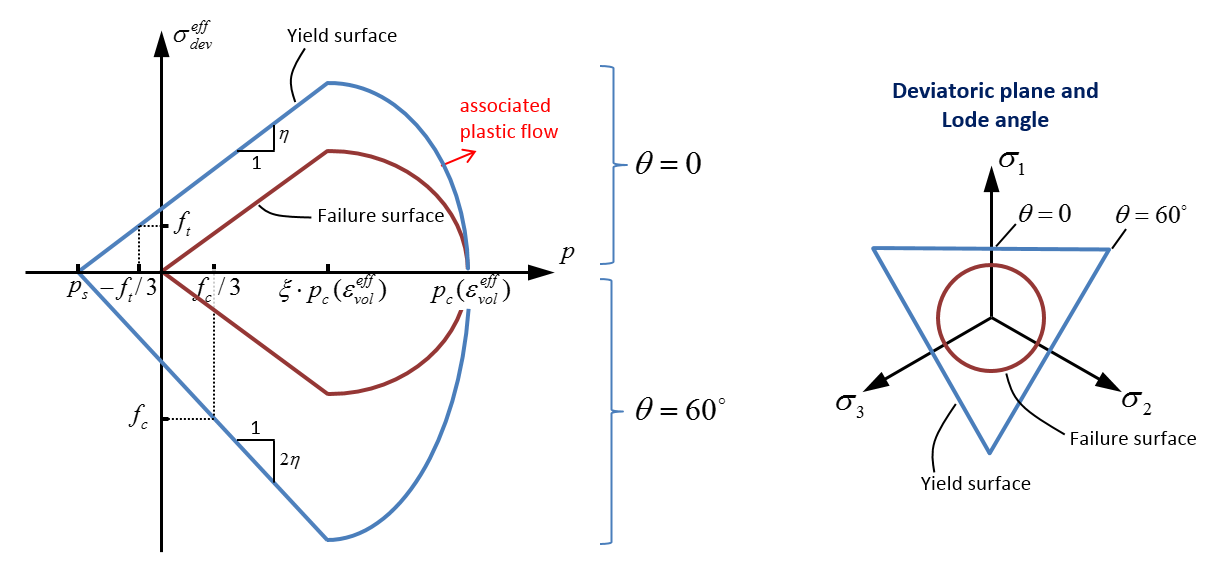
The volumetric compaction strain $\varepsilon_v^p$ can not exceed $\varepsilon_L$. The deviatoric yield stress $\sigma_y$ is defined as (se figure below):

$\sigma_y = \left\{ \begin{array}{ccc} 0 & : & p \leq p_s \\ \eta (p-p_s) & : & p_s \lt p \lt \xi p_c \\ \eta (\xi p_c-p_s) \displaystyle{\sqrt{1 - \left( \frac{p/p_c - \xi}{1 - \xi} \right)^2}} & : & \xi p_c \leq p \leq p_c \end{array} \right. $

where $\eta$ and $p_s$ (hydrostatic pressure cut-off) are derived internally to correctly match the given (quasistatic) uniaxial tensile and the compressive strengths $(f_t, f_c)$.

$\eta = \displaystyle{\frac{3}{2} \cdot \frac{f_c - 2f_t}{f_t + f_c} \cdot \frac{1}{(1-D_c) \cdot \mathrm{cos}(\theta)+D_c}}$

$p_s = -\displaystyle{\left( \frac{f_t f_c}{f_c - 2f_t} \cdot (1-D_t) + \frac{r_f (\dot\varepsilon_{eff}^p)^{r_e}}{\eta} \right) \cdot (1 - D_c) \cdot (1 - D_0)}$

$\theta$ is the Lode angle, as define in the figure below. $D_t$ is the tensile damage, $D_c$ is the crushing damage and $D_0$ is the initial defect level. Note that $p_s=0$ for a fully damaged material. Initial defects are optional and can be defined with the command INITIAL_DAMAGE_RANDOM.

The volumetric crushing damage $D_c$ is defined as:

$\displaystyle{D_c = \mathrm{min}(1, \frac{\varepsilon_v^p}{\varepsilon_c})}$

Tensile/shear cracking is controlled by the damage variable $D_t$. Node splitting is activated when $D_t$ reaches 1.

$\displaystyle{D_t = \int_0^{\varepsilon_{eff}^p} \frac{1}{\varepsilon_t}\mathrm{d}\varepsilon_{eff}^p}$

Crack propagation occurs if the first principal stress in the crack tip exceeds the fracture toughness, $K_{Ic}$.

Pressure and Lode angle dependent yield surface with cap